充足可能性問題 (satisfiability problem, SAT)
「与えられた論理式を真にする真偽値$x_1, x_2 \dots$が存在するか?」という問題を充足可能性問題という。
この問題の最も一般的な形は、NP 完全であることが知られている。
例: $(x_1 \lor x_2) \land (x_1 \lor \bar{x_2}) \land (\bar{x_1} \lor \bar{x_2})$
解: $x_1=\text{True}$, $x_2=\text{False}$
この例のように$\bigwedge_i \bigvee_j x_{i,j}$で表される論理式を連言標準形といい、その各項の変数の数が 2 以下であるとき 2-SAT と呼ばれる。 2-SAT は多項式時間で解けるアルゴリズムが存在する。 一方で項の変数の数が 3 以下の 3-SAT は NP 完全であることが知られている。
問題の生成
3-SAT 問題は DIMACS CNF で記述される。
c example DIMACS-CNF 3-SAT
p cnf 3 5
-1 -2 -3 0
1 -2 3 0
1 2 -3 0
1 -2 -3 0
-1 2 3 0
行頭がcの行はコメントである。
行頭がpの行には変数が 3 つで項数が 5 項である。
また、 -1 -2 -3 0は$\bar{x_1} \lor \bar{x_2} \lor \bar{x_3}$を示している。
つぎに、この形式の問題を機械的に作る方法を説明する。 Python の場合は次のようになる。
from numpy.random import randint, choice
def generate_3sat_sample(vn, cn):
output = "p cnf " + str(vn) + " " + str(cn) + "\n"
for i in range(cn):
a, b, c = randint(1, vn+1, (3,))
while a == b or b == c or c == a:
a, b, c = randint(1, vn+1, (3,))
s1, s2, s3 = choice([-1, 1], (3,))
a, b, c = s1 * a, s2 * b, s3 * c
output += str(a) + " " + str(b) + " " + str(c) + " 0\n"
return output
output = generate_3sat_sample(10, 42)
filepath='input.txt'
with open(filepath, mode='w') as f:
f.write(output)
vnが変数の数を表し、cnが項の数を表す。
Bash の場合は次のようになる。
vn=10
cn=42
for tmp in `seq 0 $cn`; do
if [[ $tmp == 0 ]]; then
echo "p cnf" ${vn} ${cn}
continue
fi
a= b= c=
while [[ $a == $b ]] || [[ $b == $c ]] || [[ $a == $c ]]; do
a=$(($RANDOM % $vn + 1))
b=$(($RANDOM % $vn + 1))
c=$(($RANDOM % $vn + 1))
done
a=`[[ $(($RANDOM%2)) == 0 ]] && echo $a || echo $((- $a))`
b=`[[ $(($RANDOM%2)) == 0 ]] && echo $b || echo $((- $b))`
c=`[[ $(($RANDOM%2)) == 0 ]] && echo $c || echo $((- $c))`
echo $a $b $c 0
done > input.txt
これで大量に問題が生成出来る。
問題を解く
SAT は何十年も研究されている重要な問題であるため、この問題を解くためのコマンドが公開されている。
今回はminisatを用いる。
Mac の場合はbrew install minisatで簡単にインストールが可能である。
使い方は、
$ minisat input.txt output.txt
である。 output.txt に結果が書き込まれる。
以上を組み合わせて次のようなスクリプトを作成した。
vn=100
N=9
echo "vn" "cn" "i" "sat"
for cn in `seq 10 10 1000`; do
for i in `seq 0 $N`; do
for tmp in `seq 0 $cn`; do
if [[ $tmp == 0 ]]; then
echo "p cnf" ${vn} ${cn}
continue
fi
a= b= c=
while [[ $a == $b ]] || [[ $b == $c ]] || [[ $a == $c ]]; do
a=$(($RANDOM % $vn + 1))
b=$(($RANDOM % $vn + 1))
c=$(($RANDOM % $vn + 1))
done
a=`[[ $(($RANDOM%2)) == 0 ]] && echo $a || echo $((- $a))`
b=`[[ $(($RANDOM%2)) == 0 ]] && echo $b || echo $((- $b))`
c=`[[ $(($RANDOM%2)) == 0 ]] && echo $c || echo $((- $c))`
echo $a $b $c 0
done > tmp/input.txt
minisat tmp/input.txt tmp/output.txt &> /dev/null
s=`head -n 1 tmp/output.txt`
echo $vn $cn $i $s
done
done
これをbash main.sh | tee stat.txtで実行し実験を行った。
結果
変数の数(vn)が100の 3-SAT について、条件の数(cn)を$10, 20, \cdots, 1000$と変化させて解が存在するか実験を行った。
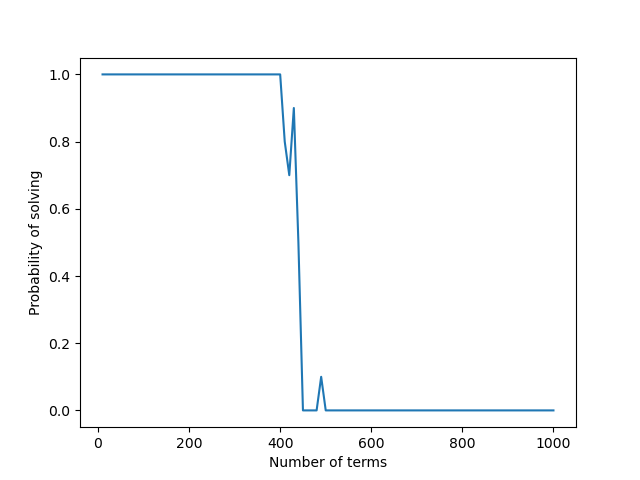
横軸は項の数(cn)であり、縦軸は解が存在する確率を表す。(分母は 10)
解の存在する確率は条件の数が 400 から 500 にかけて一気に下がることが読み取れる。
さらに詳細な実験を行った。
vn=100の場合に、cnを$400, 401, \cdots, 450$と変化させて解が存在する確率を測定した。
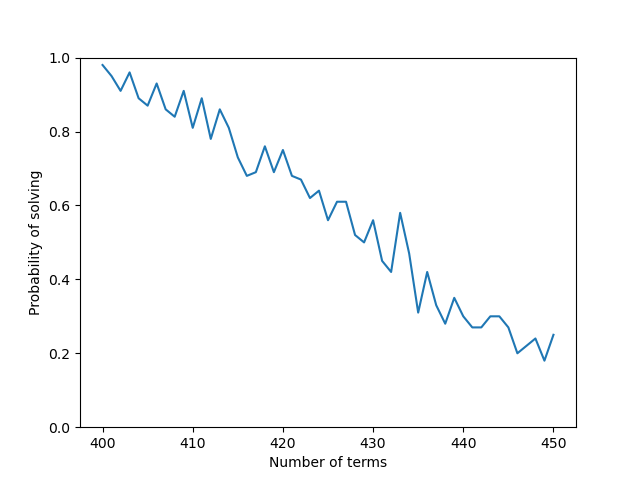
実は 3-SAT は変数の数(vn)に対して、条件の数(cn)が4.26倍のときに解ける確率が 50%になることと、その付近で最もこの問題を解くことが難しいことが知られている。
したがってこの実験結果はそれを確かにそれを反映していることがわかる。
更に、変数の数(vn)が10の 3-SAT について、条件の数(cn)を$1, 2, \cdots, 100$と変化させて解が存在するか実験を行った。
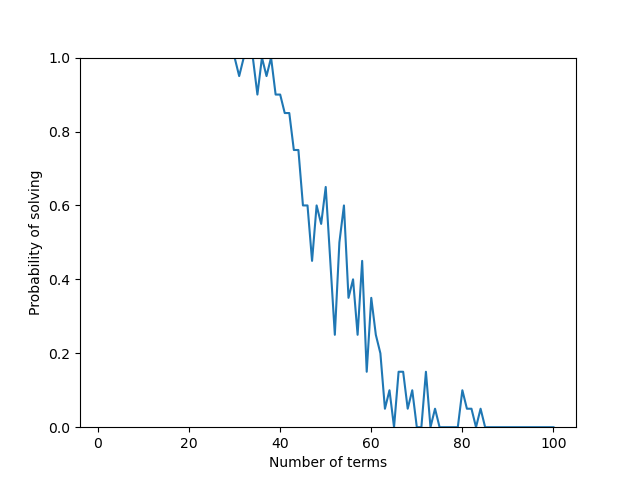
vn=100の場合とあまり形が変わらず、条件の数(cn)が4.26倍のときに解ける確率が 50%となっている傾向が読み取れる。
まとめ
- 充足可能性問題の相転移の実験をした。
- Bash の
$RANDOMが遅すぎるので、実験にかなり時間がかかった。 - 確かに、条件が少なすぎるときには解が存在することはすぐにわかり、条件が多すぎるときには矛盾を一つ見つければ解が存在しないことがすぐにわかる。そのため、その間ぐらいが一番難しいというのは普通なことな気がする。
4.26倍というマジックナンバーを導出する方法はないのかな。