1 次元のイジング模型
周期的境界条件のもとで 1 次元のイジング模型のハミルトニアンは
$$ H\left(\sigma_{1}, \cdots, \sigma_{N} \right) = -J \sum_{i} \sigma_{i} \sigma_{i+1} - h \sum_{i} \sigma_{i} $$
である。 ここで、$\sigma_{i}=\pm 1$はスピンを表し、周期的境界条件から$\sigma_{1} = \sigma_{N+1}$が成り立つ。 また$h$は外部磁場を表し、$J$は隣り合うスピンの相互作用を表す。
このハミルトニアン$H$から分配関数$Z$は
$$ Z = \sum_{\sigma_{1}, \cdots, \sigma_{N} = \pm 1} e^{- \beta H \left(\sigma_{1}, \cdots, \sigma_{N} \right)} $$
と計算出来る。 ここで、$\beta = \frac{1}{k_B T}$は逆温度である。 この分配関数は次のように書き換えることが出来る。
$$ Z = \sum_{\sigma_{1}, \cdots, \sigma_{N}} \exp{\left( \sum_i \beta J \sigma_i \sigma_{i+1} + \frac{\beta h}{2} (\sigma_i + \sigma_{i+1}) \right)} = \mathrm{tr} \left( T^N \right) $$
ここで、$T = \begin{pmatrix} e^{\beta(J+h)} & e^{-\beta J} \cr e^{-\beta J} & e^{\beta(J-h)} \end{pmatrix}$である。 さらに、行列$T$を対角化: $T=P^{-1} \Lambda P$, $\Lambda = \mathrm{diag}(\lambda_1, \lambda_2)$を計算すれば、分配関数は$Z = \lambda_1^N + \lambda_2^N$が計算出来る。
分配関数$Z$を用いて
- 自由エネルギー: $F = \frac{-1}{\beta} \log Z$
- 内部エネルギー: $E = - \frac{\partial \log Z}{\partial \beta}$
- 比熱: $C = \frac{\partial E}{\partial T}$
- 磁化: $M = \frac{1}{\beta} \frac{\partial \log Z}{\partial h}$
- 磁化率: $\chi = \left. \frac{\partial M}{\partial h} \right|_{h=0}$
のように物理量を計算出来る。 1 次元のイジングモデルの場合これらの量が厳密に計算出来ることが知られている。
この記事では、PyTorch で分配関数$Z$を計算し自動微分を用いて物理量の計算する。
PyTorch を用いた分配関数の計算
Pytorch を用いると分配関数は次のように計算出来る。
import torch
from torch import exp, pow, trace, log, tensor
def partition_function(beta, h):
J = 1.0
T = exp(beta * (tensor([[J, -J], [-J, J]]) + h * tensor([[1, 0], [0, -1]])))
Z = trace(pow(T, 10))
return Z
t = tensor(1.0, requires_grad=True)
beta = 1./t
h = tensor(1., requires_grad=True)
Z = partition_function(beta, h)
自由エネルギーは
F = -log(Z) / beta
で計算出来る。
内部エネルギー$E$と磁化$M$は$\log Z$の微分であるから、
E = torch.autograd.grad(-log(Z), beta, create_graph=True)[0]
M = torch.autograd.grad(log(Z), h, create_graph=True)[0] / beta
で計算出来る。
更に比熱$C$は内部エネルギー$E$の微分なので
C = torch.autograd.grad(E, t, create_graph=True)[0]
で計算出来る。
また、磁化率$\chi$は$\log Z$の$h$の二回微分を$h=0$における値であるから
h = tensor(0., requires_grad=True)
Z = partition_function(beta, h)
M_ = torch.autograd.grad(log(Z), h, create_graph=True)[0] / beta
x, = torch.autograd.grad(M_, h, create_graph=True)
で計算出来る。
以上のようにすべての物理量を PyTorch の自動微分の機能で計算はできる。
物理量の温度変化を可視化
物理量の温度変化を計算する。 手計算でも行える計算を自動微分を用いて数値計算しているだけなので結果は正しいはず。
import torch
from torch import exp, pow, trace, log, tensor
import numpy as np
import matplotlib.pyplot as plt
def partition_function(beta, h):
J = 1.0
T = exp(beta * (tensor([[J, -J], [-J, J]]) + h * tensor([[1, 0], [0, -1]])))
Z = trace(pow(T, 10))
return Z
data = []
for i in range(1, 50):
t = tensor(float(i), requires_grad=True)
beta = 1. / t
h = tensor(1., requires_grad=True)
Z = partition_function(beta, h)
F = -log(Z) / beta
E, = torch.autograd.grad(-log(Z), beta, create_graph=True)
C, = torch.autograd.grad(E, t, create_graph=True)
M = torch.autograd.grad(log(Z), h, create_graph=True)[0] / beta
h = tensor(0., requires_grad=True)
Z = partition_function(beta, h)
M_ = torch.autograd.grad(log(Z), h, create_graph=True)[0] / beta
x, = torch.autograd.grad(M_, h, create_graph=True)
data.append([t.item(), beta.item(), F.item(), E.item(), C.item(), M.item(), x.item()])
data = np.array(data).T
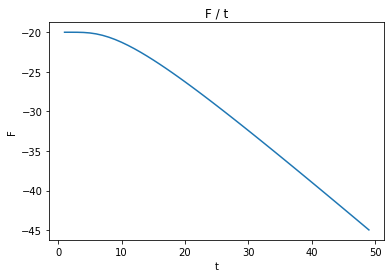
自由エネルギー: $F$
plt.title("F / t")
plt.xlabel("t")
plt.ylabel("F")
plt.plot(data[0], data[2])
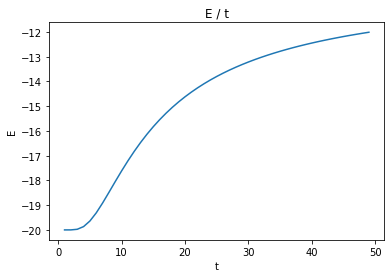
内部エネルギー: $E$
plt.title("E / t")
plt.xlabel("t")
plt.ylabel("E")
plt.plot(data[0], data[3])
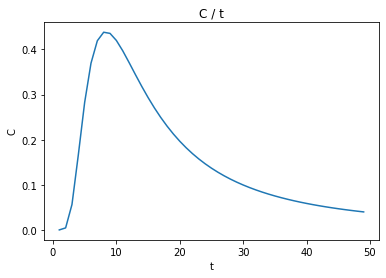
比熱: $C$
plt.title("C / t")
plt.xlabel("t")
plt.ylabel("C")
plt.plot(data[0], data[4])
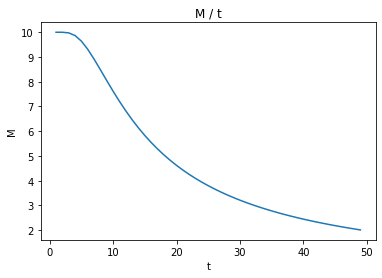
磁化: $M$
plt.title("M / t")
plt.xlabel("t")
plt.ylabel("M")
plt.plot(data[0], data[5])
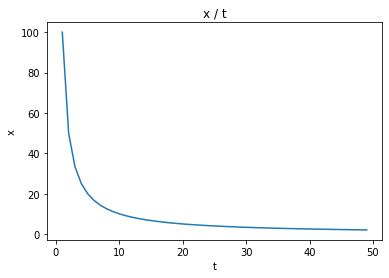
磁化率: $\chi$
plt.title("x / t")
plt.xlabel("t")
plt.ylabel("x")
plt.plot(data[0], data[6])
まとめ
- 自動微分を用いて分配関数を微分してみた。
- 今回は分配関数が微分可能演算のみで構成されているために、自動微分を用いて微分が出来た。さらに複雑なモデルでも分配関数が微分可能な計算のみで構成されていれば、物理量を計算が出来ると思う。
- 分配関数$Z=\sum_i e^{-\beta H_i}$は指数関数を大量に足し合わせる計算なので、実は簡単に Float の限界に到達してしまう。なのでもっと大きなモデル($n=100$とか)を計算するにはパラメータをうまく調整して Float に納める必要がある。
- 今回も自動微分ライブラリを機械学習以外の目的で利用して遊んでみた。他の遊び方も見つけ次第記事にしたい。