先日、三角ゲームというゲームを知った。 今回はこのゲームを Pytorch を用いて解いてみた。
三角ゲームの説明
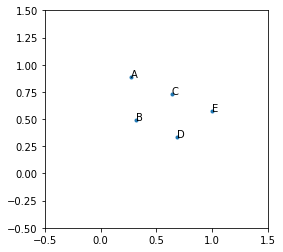
はじめに三角ゲームについて説明する。 例として$n=5$人($A, B, C, D, E$)で遊ぶ場合を説明する。
ゲームを始める前にそれぞれのプレイヤーは、自分以外の異なる2人のプレイヤーを選択する。 ここでは、$A = (B, C)$, $B = (A, C)$, $C = (B, D)$, $D = (C, E)$, $E = (C, D)$を選んだとする。 それぞれのプレイヤーは選択したプレイヤーと正三角形を作るように移動を行う。 最終的にこの条件をなるべく満たしながら最も多くの正三角形を作成することがこのゲームの目標である。
この例では以下のようにそれぞれのプレイヤーが移動すれば、すべての条件を満たし最大の 5 個の正三角形が作成出来る。
PyTorch を使って解く
このゲームを PyTorch を用いて解いてみる。
ライブラリのインポート
はじめに、準備としてライブラリのインポートと保存用の関数を用意。
import torch
from torch import norm, dot, abs
from random import randrange, random
import matplotlib.pyplot as plt
def savefig(xs, ys, i):
plt.figure(figsize=(8,8))
plt.xlim([-0.5, 1.5])
plt.ylim([-0.5, 1.5])
plt.scatter(xs, ys, marker=".")
plt.savefig("fig/fig"+str(i).zfill(5)+".png")
plt.close()
import で error が出たらpip3 install torch matplotlibする。
savefig(xs, ys, i)は、座標のリスト(xs, ys)を取得して、図を作成しfig/fig000i.pngに保存する。
ゲームの準備
次はゲームの準備を行う。
まず条件を決定する。 今回は自分以外の異なる二人のプレイヤーをランダムに選ぶ。
# determine conditions
n = 10 # プレイヤーの人数
conditions = []
for i in range(n):
a, b = randrange(n), randrange(n)
while a == i or b == i or a == b:
a, b = randrange(n), randrange(n)
conditions.append([a, b])
conditions = torch.tensor(conditions)
最終的にconditions.shape = (n, 2)である。
conditions[i]=[a, b]はプレイヤー$i$はプレイヤー$a, b$と正三角形を作成するという条件である。
次に、それぞれのプレイヤーの初期位置を設定する。
# initial positons
pos = torch.tensor([[0.8*random() + 0.1 for _ in range(2)] for _ in range(n)], requires_grad=True)
$x$座標も$y$座標も 0.1~0.9 の範囲で一様分布になるように定めている。
また、後に位置を自動微分を用いて位置を調整するので、requires_grad=Trueを設定しておく。
損失関数の定義
損失関数を定義し、この関数が最小(0)になったとき、すべての条件が満たされ正三角形が最大個数生成される。
# define loss
def loss_func(pos):
loss = torch.sum(torch.where(pos>1, pos-1, torch.zeros(pos.shape)))
loss += torch.sum(torch.where(pos<0, -pos, torch.zeros(pos.shape)))
for i, [a, b] in enumerate(conditions):
x, y, z = pos[i], pos[a], pos[b]
loss += abs(dot(y-x, z-x)/norm(y-x)/norm(z-x) - 0.5)
loss += abs(dot(z-y, x-y)/norm(z-y)/norm(x-y) - 0.5)
loss += abs(dot(x-z, y-z)/norm(x-z)/norm(y-z) - 0.5)
return loss
はじめの二行は座標が 0-1 の範囲に収まるように加えている。 あとは条件の三角形のすべての角度が 60° になるように設定している。
最適化
すべてのプレイヤーの位置posを、損失関数loss_funcが最小になるように最小化して最適化を行う。
# train
trace = [] # to trace loss
opt = torch.optim.Adam([pos], lr=0.01)
for i in range(100):
xs = pos[:, 0].detach().numpy() # to numpy
ys = pos[:, 1].detach().numpy() # to numpy
savefig(xs, ys, i) # save fig
opt.zero_grad()
loss = loss_func(pos)
trace.append(loss.item()) # trace loss
loss.backward()
opt.step()
Adamを用いてposを最適化する。
loss_funcが PyTorch の関数のみで構成されているため、posの自動微分を行うことができ効率的に最小化出来る。
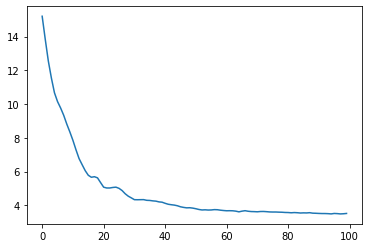
可視化
traceとposを可視化する。
# plot trace
plt.plot(trace)
# plot pos
plt.figure(figsize=(4,4))
plt.xlim([-0.5, 1.5]);plt.ylim([-0.5, 1.5]);
xs = pos[:, 0].detach().numpy()
ys = pos[:, 1].detach().numpy()
plt.scatter(xs, ys, marker=".")

conditions = [[9, 8],[8, 6],[7, 9],[2, 1],[6, 3],[6, 1],[0, 2],[8, 1],[2, 7],[6, 4]]
また、fig/に保存した画像たちは$convert fig/fig*0.png out.gifを用いて gif 動画に変換出来る。
その他の結果
$n=10$の場合と$n=100$の場合に実験を行い、動画の作成して YouTube にアップロードした。
この動画の$n=10$の場合は上手に最適化されてすべての条件を満たしている、$n=100$の場合は何がなんだかよくわからない。
感想
- 自動微分を用いて三角ゲームの最適化を行った。
- 今回の問題は必ず答えがあるわけではないので結果は微妙になってしまったが、損失関数を調整することで目に見えるいい結果が得られるかもしれないと思った。
- 自動微分は機械学習のモデルを最適化するためによく使われているが、他にも色々な遊び方がありそうだと思ったのでこういうゲームを解いてみた。
- 微分可能プログラミングも勉強してみたい。